What are Mnemonic Phrases?

The basis for generating keys and addresses is randomness. Ownership on the blockchain is highly secure, as long as the private key cannot be reproduced by an adversary.

The private key is the basis of the public key and address(es). As such, it requires a high level of security, and needs to be generated from a high level of entropy.

Generating Entropy and a Mnemonic Phrase

There are different sources for entropy:

• Hardware
• User input
• Microphone
• And camera inputs.

Preferably, some of the entropy is hardware based and uses more than a single source. Human based entropy is usually less random and therefore less secure.

The initial entropy is used as a seed for a deterministic random bit generator (DRBG), also called pseudorandom number generator (PRNG).

DRBGs should be standardized and validated. One example for a vetted algorithm is the NIST SP800-90A compliant method. The deterministic random bit generator produces a seed, which we then use to generate your mnemonic phrase.

What is a Mnemonic Phrase?

Your mnemonic phrase is a backup of your private key that is used by most wallets, it is a list of random words given to you when creating a wallet.

If you break or lose a device with a wallet - no matter if mobile, desktop or hardware wallet - your mnemonic phrase is usually your last line of defense against a loss of funds.

This implies that any attacker that gets their hands on your recovery phrase will be able to do the same. Therefore, you must protect your mnemonic phrase as well as you would protect your funds themselves.

You should write the phrase of words down on paper or save them in any analog format you see fit.

The mnemonic phrase mechanism that you are likely familiar with was introduced with the Bitcoin Improvement Proposal 39, or BIP-0039.

A mnemonic phrase uses commonly known words, which are used to provide a less error-prone backup mechanism than writing down your private key in a format like:

• Base58
• Hexadecimal
• or Binary

In total, there are 2048 words a mnemonic phrase may comprise, each of them unambiguously identifiable by its first four letters.

Similar words or different versions of the same word are not included, for example:

• build/built
• woman/women

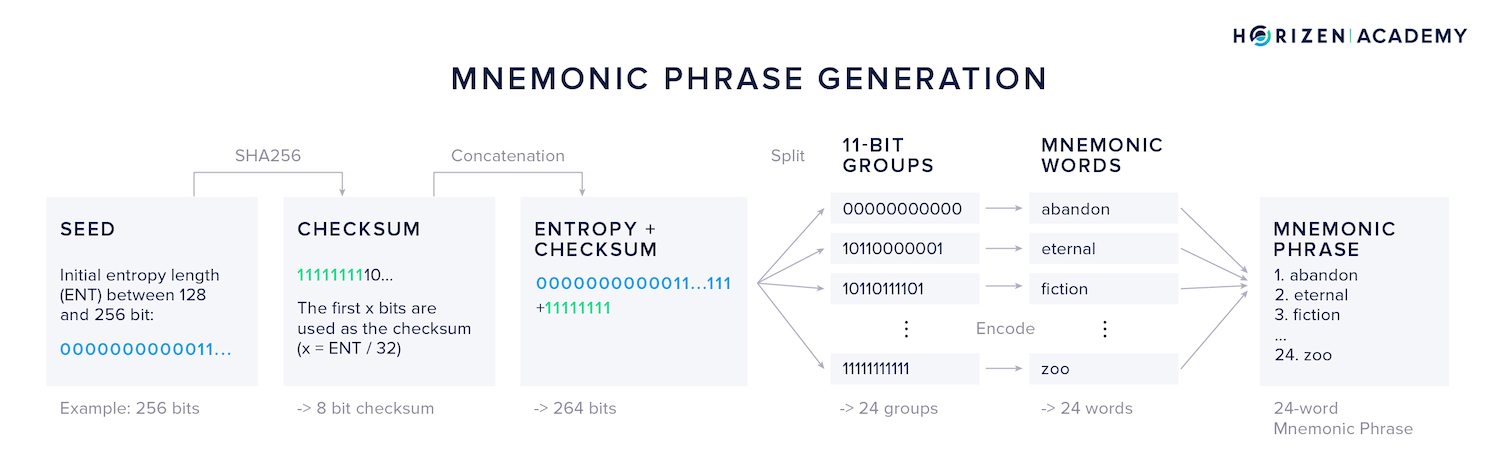
Generating a Mnemonic

1. First, a multiple of 32 bits, between 128 and 256 bits total, is generated. Let’s use an example with a 256-bit seed.
2. Second, a checksum is calculated by SHA256-hashing the seed. The first x bits of the checksum are appended to the end of the seed and x is the number of initial bits divided by 32. Using a 256-bit seed, this results in an 8 bit checksum.
3. Third, the concatenated bits are split into groups of 11 bits each. We get 24 groups for our example.
4. Next, each 11 bit group is “translated” into the corresponding word from the list of mnemonic words. 11 bits can encode the values between 0 and 2047, each matching a word in the list of 2048 words.

Now that we have a mnemonic phrase, it needs to be converted into a binary seed.

The PBKDF2 function takes the mnemonic phrase as the password and the string mnemonic + passphrase as the salt.

PBKDF2 takes this input and applies a pseudorandom function - here HMAC-SHA512 - to it, in this case 2048 times. The final output is the derived seed of 512 bits length.

This seed can now be used as an input for different key derivation methods, such as the hierarchical deterministic key derivation.

Key Derivation

Going forward, we'll use the term key generation to refer to the random generation of private keys and key derivation to refer to the path from a private key to the public key and an address.

There are instances when it is desirable to be able to generate different addresses from a single seed or private key. By using a new address for each incoming transaction, as well as to change outputs, your privacy is enhanced because it becomes harder to link transactions to a single user.

There are different approaches to get those addresses.

One could go through the entire process of key generation and derivation for each address, but this would require the user to keep backups for each individual key. This approach is called non-deterministic key generation.

While this approach mitigates the risk of losing all your funds at once in the case you lose a private key and/or mnemonic phrase, it certainly makes for a bad user experience.

Being able to securely produce several child keys from a single parent key creates a better UX in basic wallets, and also allows multi-currency wallets to be backed up with a single mnemonic.

This single mnemonic derives a key pair for each chain.

Hierarchical Deterministic Wallets

Hierarchical Deterministic Wallets were introduced with BIP-0032. The general idea is to take a master private key and use it to generate multiple secure child keys.

Before we dive into different key derivation methods, we need to introduce a concept we’ve omitted thus far.

The 512-bit seed we obtained from our mnemonic phrase by applying the PKKDF2 function is split into two parts:

1. A zero-level private key
2. and a 256-bit chain code cc

The chain code is used as a key to the HMAC-SHA256 pseudorandom function that takes two pieces of input, the data and a key, to produce a single 512-bit output.

The HMAC-SHA256 function is used at several steps in the key derivation process.

To recap what we did thus far:

• We generated a random bit sequence and used it as an input to a deterministic random bit generator that produced a seed.
• From this seed, we generated a mnemonic phrase, which in turn was converted into a 512-bit binary seed.
• We split our seed into the zero-level private key \(sk_0\) and the zero-level chain code \(cc_0\). A zero-level public key \(PK_0\) is generated from \(sk_0\) using elliptic curve cryptography

Hardened vs. Non-Hardened Secret Key Derivation

When looking at the key derivation in HD wallets, we can generally differentiate between hardened secret key derivation (HSKD) and non-hardened secret key derivation (NSKD).

The difference lies in the inputs used to generate first-level keys.

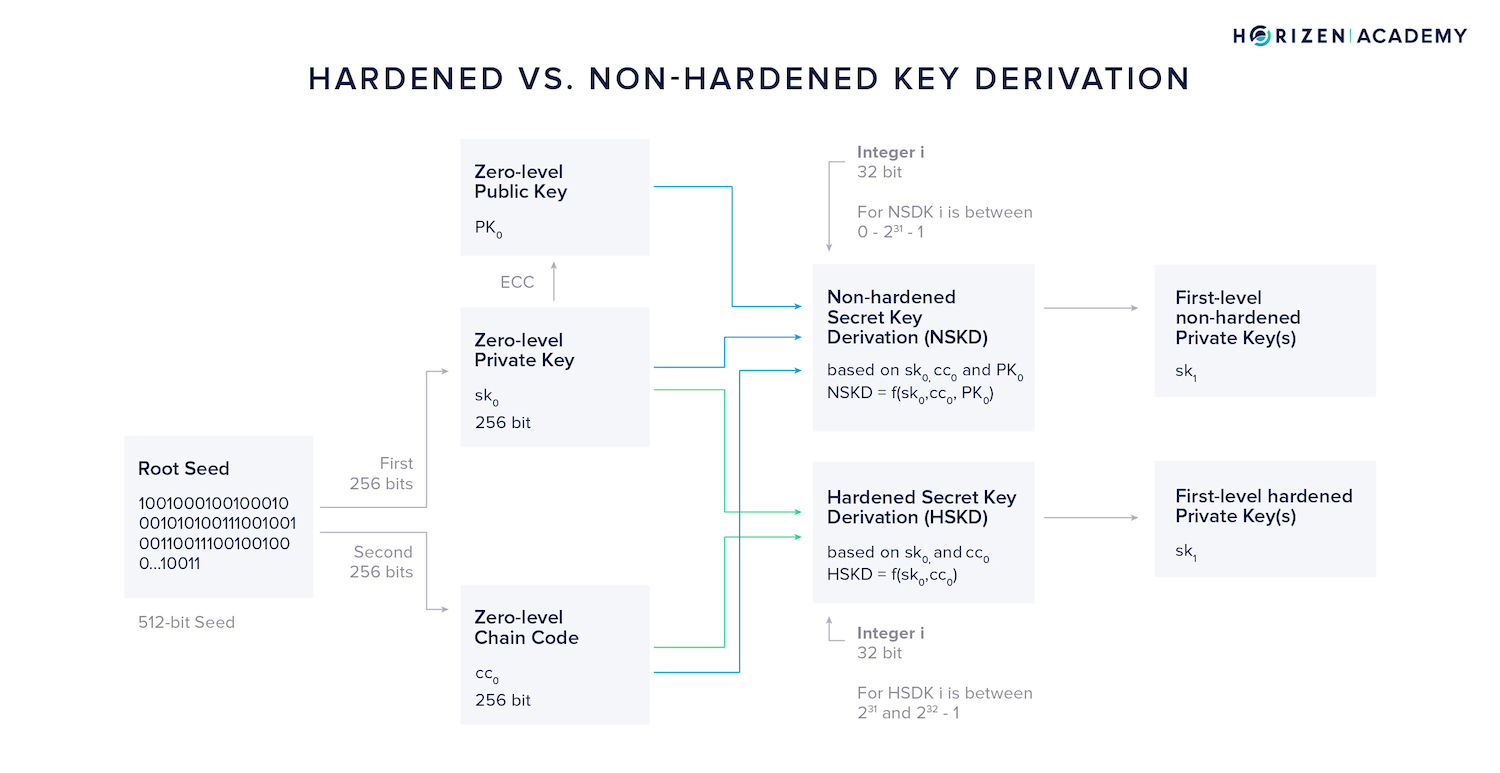
Additionally, we need to introduce the variable i at this point. It is a 32-bit integer that is used to derive different keys with index i from a single zero-level key.

By convention, the total range of possible values of i is split between HSKD and NSKD, giving both methods the option to create 2147483648 different first-level keys from a single zero-level key.

The hardened secret key derivation takes the zero-level private key \(sk_0\), the zero-level chain code \(cc_0\) and the integer i as an input.

By convention, the top of the integer range, from \(2^{31}\) to \(2^{32}-1\), of i, is used for the hardened secret key derivation method.

In other words, using the HSKD method, the first-level private key \(sk_1\) is a function of three values:

$$ sk_1 = HSKD(sk_0, c_0, i) $$

The non-hardened secret key derivation (NSKD) additionally takes the zero-level public key \(PK_0\) into account. In the non-hardened secret key derivation method, i will by convention take on values between 0 and \(2^{31}-1\), so the lower half of the total range of i.

In other words, using the HSKD method the obtained first-level private key \(sk_1\) is a function of four values:

$$ sk_1 = NSKD(sk_0, PK_0 c_0, i) $$

Hardened Secret Key Derivation - HSKD

The core function that the key derivation is build around is the hash-based message authentication code (HMAC). It is a specific type of message authentication code involving a cryptographic hash function and a secret cryptographic key.

It always uses some hash function, which is then appended to name the exact function. In this specific case, the SHA512 hash function is used and the message authentication code is called HMAC-SHA512.

HMAC consumes several inputs. For our purposes we group them into two: the key and the data.

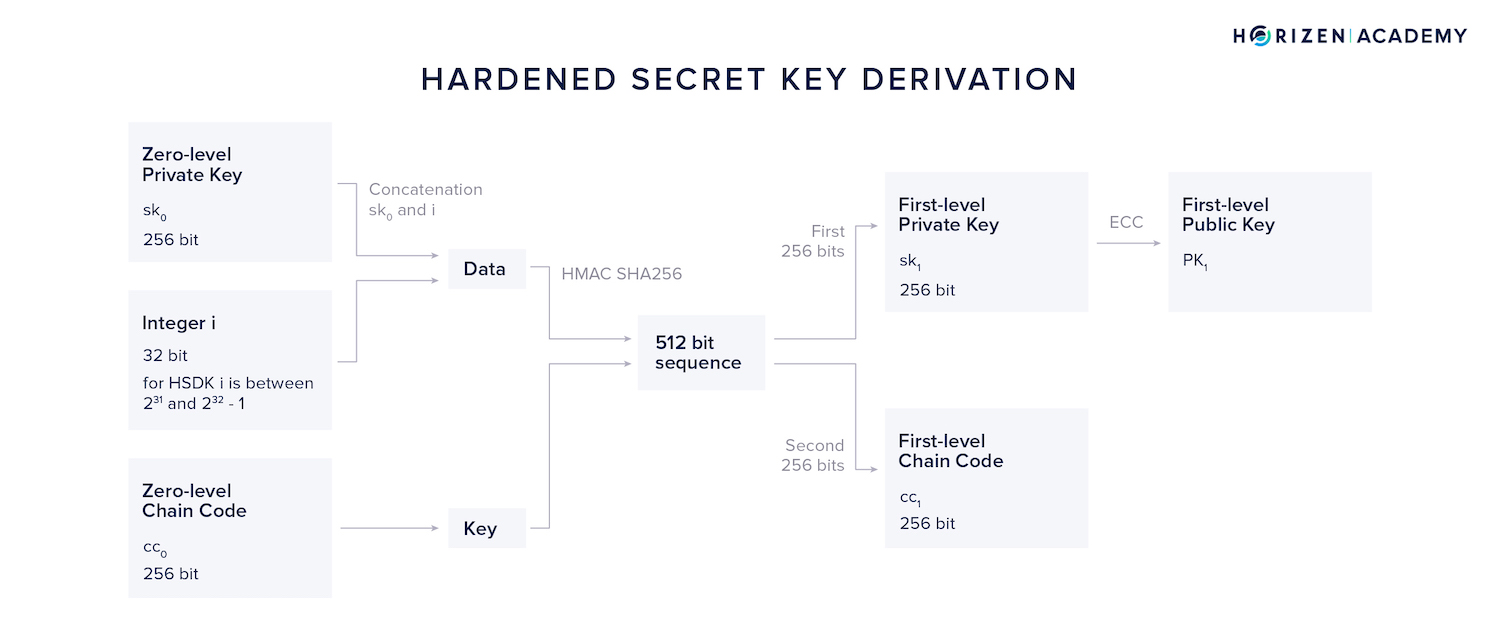
For the HSKD method, the concatenation of \(sk_0\) and our variable integer i is used as the data and the zero-level chain code \(c_0\) as the key.

The resulting 512-bit output is split into two parts of 256 bits each.

• The first half becomes our first-level private key \(sk_1\)
• The second half our first-level chain code \(cc_1\).

By applying elliptic curve cryptography to \(sk_1\) we can obtain our first-level public key \(PK_1\).

By incrementing i we can generate \(2^{31}\) or 2147483648 different first level private keys and chain codes.

Non-Hardened Secret Key Derivation - NSKD

We can also derive a first level private key using a combination of our zero-level public key \(PK_0\), zero-level secret key \(sk_0\) and our zero-level chain code \(cc_0\).

This method is called Non-Hardened Secret Key Derivation (NSKD).

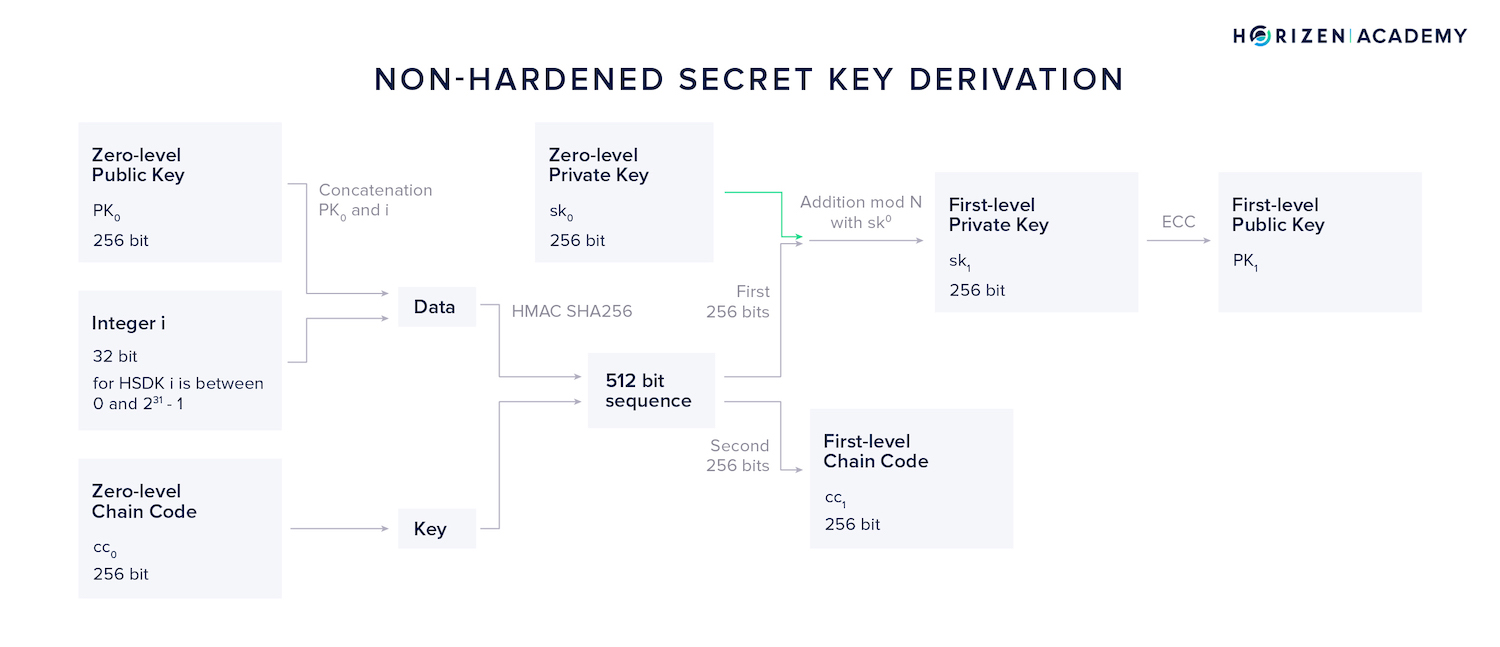
Again, we will use the HMAC-SHA256 function, but this time we use the concatenation of \(PK_0\) and i as out data and once again \(cc_0\) as our key.

Again, the resulting 512-bit output is split into two parts of 256 bits each. While the second part becomes our first level chain code \(cc_1\) as it did in the HSKD method, the first 256 bits are handled differently.

It doesn't yield our first level private key directly, but instead an addition modulo N with the initial private key \(sk_0\) is performed in order to obtain the first level private key.

Lastly, ECC is used to generate our first level NSKD public key \(PK_1\).

Now imagine a case where a large number of addresses, or public keys respectively, need to be generated on a continuous basis - think a merchant accepting crypto payments.

Both methods described before, HSKD and NSKD need access to the zero-level private key to compute new child keys and hence addresses.

The zero-level private key is also the key that will allow the merchant to spend the money they received, so they should never host this process on the same server that the payment logic resides on. Meet NPKD - the Non-Hardened Public Key Derivation method.

Non-Hardened Public Key Derivation - NPKD

Using the Non-Hardened Public Key Derivation method, our zero level private key \(sk_0\) isn't needed at all. The first steps in the NPKD method are analogous to the NSKD method.

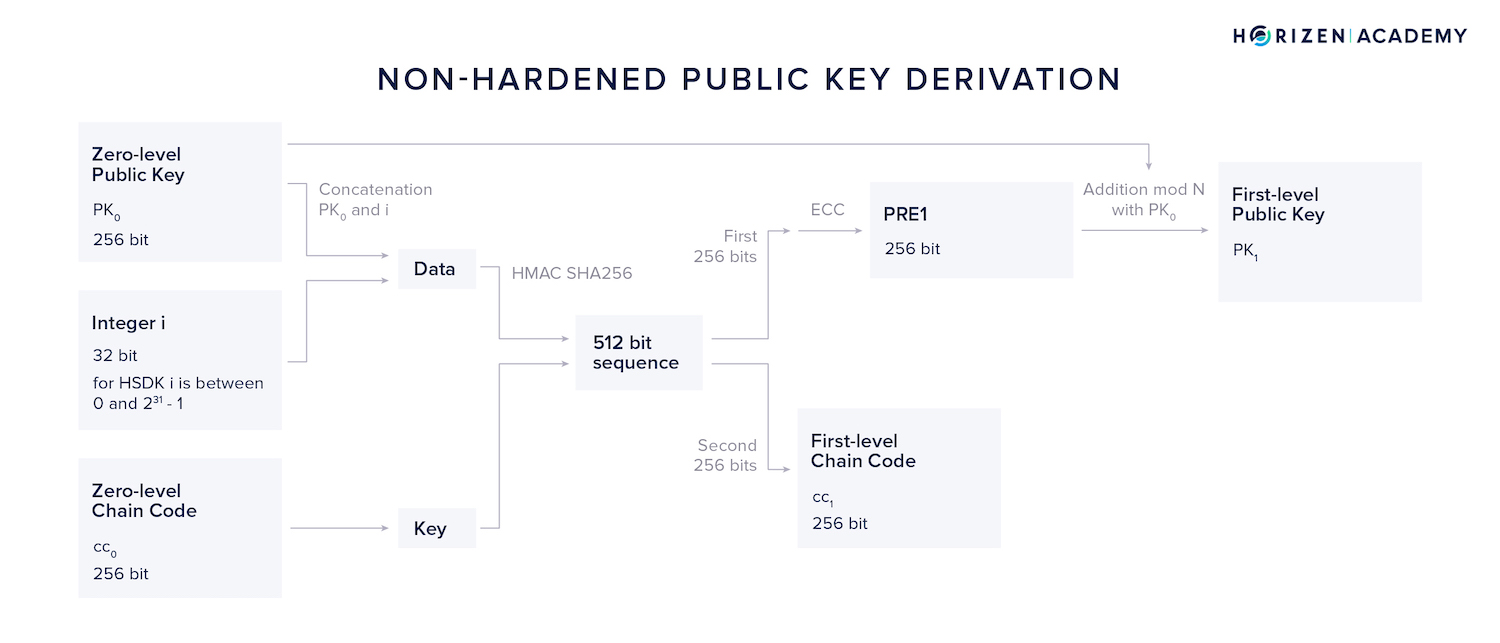
The concatenation of \(PK_0\) and i is used as data and \(cc_0\) as our key. Again, the resulting 512-bit output is split into two parts of 256 bits.

The first 256 bits are used as an input to the ECC module, producing an intermediary result we call \(PRE_1\).

Applying the addition module N together with our zero-level public key \(PK_0\) we get a first level public key \(PK_1\) without having to touch \(sk_0\) at all.

Spending funds received at an address derived from a first-level public key yielded from this method works with \(sk_0\), as the first-level public key obtained using NPKD is equivalent to the first-level public key produced with the NSKD method.

Summary - Mnemonic Phrases

The mnemonic phrase is a list of words that can be used to restore your private key. The mnemonic phrase is as sensible as your private key itself and if it gets in the wrong hands, your money can be stolen.

This should not scare you, but make you cautious.

The first step in generating keys is to produce a random private key. Different sources for entropy generation can be used, and it’s advisable to use several sources of entropy for added security.

Mnemonic phrases are generated by splitting the initial entropy into groups and mapping each group to a word.

There are different ways to derive a public key from a private key, the difference being the type of inputs. Most wallets today are hierarchical deterministic wallets that can create several key pairs from an initial entropy source.

This is good for the user because they only need a single key to generate several separate accounts, even across different blockchains.